GeoDa Yazılım – En İyi Veri Keşfi

GeoDa Yazılım

Bu sizin keşfetmek için eğlenceli GeoDa ile ta GeoDa .

MIT, Chicago ve Arizona gibi üniversiteler, güçlü mekansal veri analizi, coğrafi görselleştirme ve jeoistatistik araçları nedeniyle GeoDa’yı kullanıyor.

Biz de öyle yaptık.

GeoDa yazılımını Spatial @ UChicago’dan nasıl indireceğiniz aşağıda açıklanmıştır. Şimdi, yeni ve geliştirilmiş GeoDa’daki temel özellik olup olmadığını kontrol edelim.

GeoDa’ya Başlarken

GeoDa, şekil dosyası, GeoJSON, KML, SQLite ve tablo formatı (CSV, XLS ve DBF) gibi birden çok dosya formatını eklemenizi kolaylaştıran sezgisel bir arayüze sahiptir.

Coğrafi verilerinizin uzayda nasıl ilişkili olduğunu görmek için GeoDa, Carto ve Nokia’dan çeşitli temel haritalar sağlar.

Aşağıda gösterildiği gibi, bu 4 araç verileri yüklemek, GeoDa projesi (GDA) olarak kaydetmek, uygulamayı kapatmak ve öznitelik verilerini açmak için kullanılır.

Herhangi bir CBS yazılımına benzer şekilde, sütunları serbestçe yeniden boyutlandırabilir ve taşıyabilirsiniz. Tabloları, sorgu gözlemlerini birleştirebilir ve verileri farklı formatlarda dışa aktarabilirsiniz.

Söylenecek fazla bir şey yok ama GeoDa’yı kullanmak için ne kadar açık sözlü bulduk. Arayüz moderndir ve analizlerinizde ellerinizi çabucak kirletebilirsiniz.

 

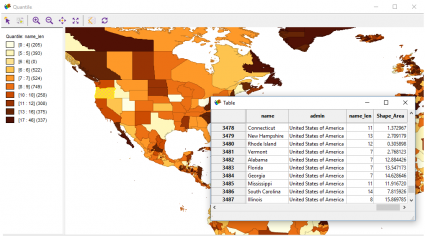
Coğrafi Görselleştirme ve Veri Sınıflandırma

Bu GeoDa’nın uzmanlık alanlarından biridir – coğrafi görselleştirme araçları. Tematik haritalar, kartogramlar ve harita filmleri biçimindeki görselleştirmeler yoluyla herkes verilerinde içgörü kazanabilir.

Gerçekten, veri sınıflandırması açısından QGIS ve ArcGIS’ten daha fazla seçenek elde edersiniz. Haritalar ve hızı açılan size bir verir bolluğu verilerinizi sınıflandırmak için yollar.

• Temasız Harita – Basit tek renkli harita
• Quantile Map – Grupları aynı miktara sahip olacak şekilde düzenler.
• Yüzdelik Eşlem – Farklı yüzdelik dilimlerde verileri gölgeler (% 99)
• Kutu Haritası – Aykırı değerlerin farklı şekilde gölgelendirildiği bir çeyrek haritası.
• Standart Sapma Haritası – Her standart sapma bir sınıf haline gelir.
• Benzersiz Değerler Haritası – Değerleri benzersiz şekilde kategorilere ayırır.
• Natural Breaks Haritası – Her grubu, her sınıfta daha az varyasyon olacak şekilde düzenler.
• Eşit Aralıklı Harita – Sınıfları eşit gruplara ayırır.
• Oranlar-Hesaplanan Harita – Verileri sınıflandırmak için uzamsal ağırlıkları kullanır.

DAHA FAZLASINI OKUYUN: Choropleth Haritaları – Veri Sınıflandırma Rehberi

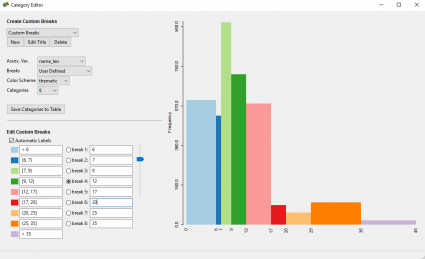
Bu tür veri sınıflandırma yöntemlerini kullanmak istemiyorsanız, GeoDa’nın verilerdeki özel kesmeleri etkileşimli olarak düzenlemeniz için bir Kategori Düzenleyici aracı vardır. Güzel olan şey, verilerinizdeki bölme çizgilerini değiştirirken etkileşimli olarak nasıl bir histogram oluşturduğudur.

Kartogram aracı, bir değişkeni temsil etmek için uygun boyutlu dairelerin yerini alır. Örneğin, burada Amerika Birleşik Devletleri’ndeki nüfus kümelerini görüyoruz.

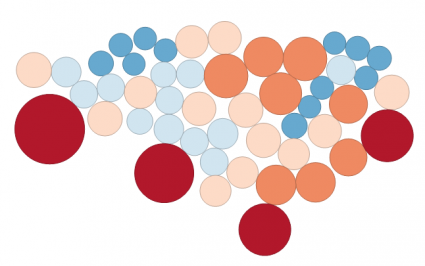
Bu aynı zamanda Dorling Kartogramları olarak da bilinir. Bununla birlikte, bu tür kartogramların dezavantajı, ağırlık merkezi ve şeklin korunmamasıdır. Bu, okuyucuların haritadaki özellikleri anlamakta güçlük çekebileceği anlamına gelir. Size söylemeseydim, bunun Birleşik Devletler nüfusunu temsil ettiğini bile bilmiyor olabilirsiniz!

 

Veri Keşfi Analizi

Bu bölüm için, St Louis bölgesi ilçe cinayet sayılarını ve oranlarını kullanarak bazı istatistiksel ilişkileri araştıracağız.

İnceleyeceğimiz üç ana değişken şunlardır:

• HR8488 – 100.000’de cinayet oranı
• PE87 – kişi başına polis harcamaları
• RDAC85 – kaynak yoksunluğu / refah bileşik değişkeni (yoksulluk sınırının altında yaşayan ailelerin yüzdesi, ortalama aile geliri)

DEVAMINI OKU: Chicago Üniversitesi Örnek Veri Kümeleri (Harika örnek veriler)

Histogram

Polis harcamalarının bu histogramına baktığınızda, paranın nasıl harcandığının ilçelere göre dağılımının nispeten eşit olduğunu görebilirsiniz.

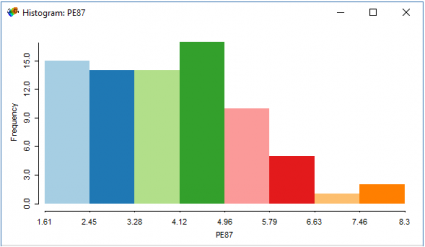
Ancak cinayet oranlarının histogramına baktığınızda, olumlu bir şekilde çarpık. Bu, verilerin çoğunun cinayet oranının düşük olduğu anlamına gelir, ancak son derece yüksek cinayet oranlarına sahip bazı ilçeler vardır.

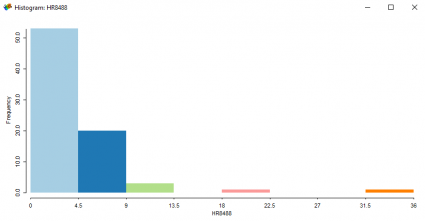
Kutu Grafiği

Bu kutu grafiği, 100.000 kişi başına düşen ortalama cinayet sayısının yaklaşık 3,7 olduğunu gösteriyor. Bununla birlikte, muazzam cinayet oranlarıyla gerçekten sıçrayan iki ülke var. Bu iki bölge St. Louis City (36.0) ve St. Clair (20.2) ‘dir.

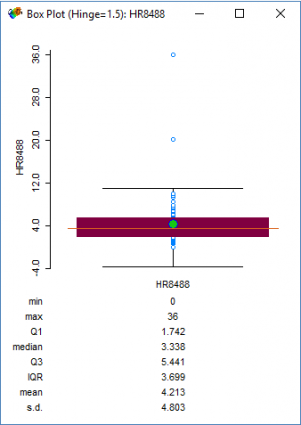
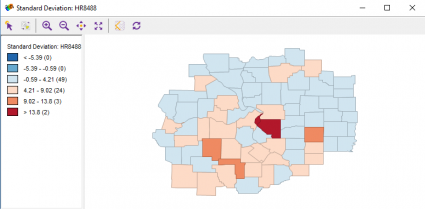
Bu iki gözlem tam olarak nerede? Standart sapma türü bir haritada, burada normalden daha yüksek cinayet oranlarına sahip iki ilçeyi kırmızıyla boyadık. Gördüğünüz gibi, cinayet oranının ortalamasından daha büyük 3 standart sapmaları var.

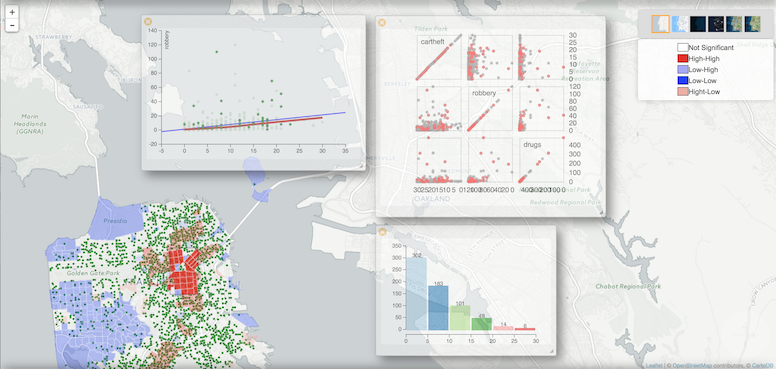
Dağılım grafiği

Değişkenlerin birbirleriyle nasıl ilişkili olduğunu görmenin en iyi yolu nedir? Örneğin, kaynak yoksunluğu / refah bileşik değişkeni cinayet oranlarıyla nasıl ilişkilidir?

Her değişkeni bir grafiğin x eksenine ve y eksenine yerleştirebiliriz ve nasıl göründüğünü görebiliriz. Buna dağılım grafiği denir.

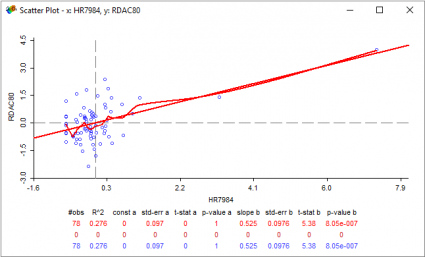
Doğrusal regresyon eğrisi (düz kırmızı çizgi) bize 0.276’lık bir r-kare değeri verir. Diğer kırmızı eğri çizgi, bu iki değişken arasında düzgün bir eğriye uyan bir DÜŞÜK (LOcally WEighted Scatter-plot Smoother) ‘dir.

Peki bu aslında ne anlama geliyor?

Bu 78 gözlem göz önüne alındığında, kaynak yoksunluğunun cinayet oranlarındaki varyansın% 27,6’sını oluşturduğu anlamına gelir. R-karesi sıfır olan bir model% 0’ı gösterirken, bir model yanıt verilerinin ortalamasına göre hiçbir değişkenliğini açıklamaz… Bu gerçekten bu iki değişken (kaynak yoksunluğu ve cinayet oranları) arasında kısmi bir ilişki olduğunu gösterir.

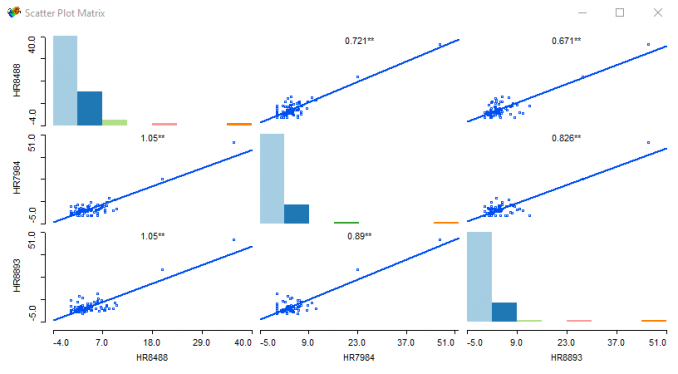
Ama gerçekten burada GeoDa ile bitmiyor. Bir grup dağılım grafiğinin birbiriyle nasıl ilişkili olduğunu görmek istiyorsanız, kalbinizin istediği tüm değişkenleri Dağılım Grafiği Matrisi ile seçin.

3B Dağılım Grafiği

Geoda’nın 3B dağılım grafiği için gerçekten düşünme sınırınızı takmanız gerekecek. En azından yaptım. Bu aracın yaptığı şey, bunun gibi üç boyutlu uzayda üç ayrı değişkenin grafiğini çıkarmaktır.

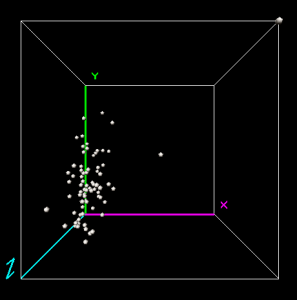
Bununla ilgili güzel olan şey, veri noktalarınızı XY eksenine, XZ eksenine veya ZY eksenine nasıl yansıtabileceğinizdir. 3B Dağılım Grafiğini döndürerek verilerin her eksende nasıl göründüğünü gördüğünüzde. Bu noktada, veri noktalarının 3B alanda nasıl askıya alındığını anlamaya başlayacaksınız.

Kabarcık Grafikleri

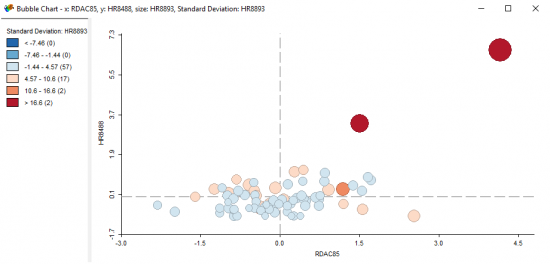
Kabarcık grafikleri için, X ve Y ekseni değişkenlerini seçersiniz. Buna ek olarak, kabarcık boyutu ve rengi için bir değişken seçersiniz. Bunun yapmanızı sağladığı şey, dört değişkeni akıllıca bir şekilde görselleştirmektir.

Grafiğinizi gerçekten etkileyebileceğinden boyut değişkenine dikkat edin. Grafiği sağ tıklayıp balon boyutunu küçükten büyüğe yeniden boyutlandırabilirsiniz. Burada işi basit tutuyoruz ve cinayet oranlarını boyut olarak kullanıyoruz. Beklendiği gibi, iki büyük kırmızı baloncuk St. Louis City ve St. Clair’dir.

Paralel Koordinat Grafiği (PCP)

Yeni favori grafiğimle tanışın.

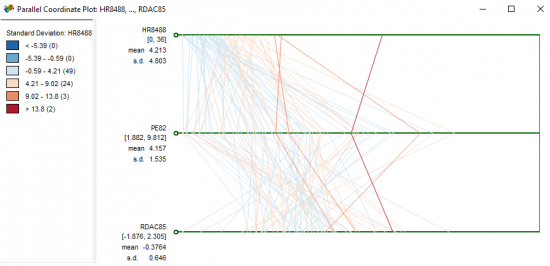
Bir Paralel Koordinat Grafiğinde, her satır, cinayet oranları, polis harcamaları ve kaynak yoksunluğu planlanmış bir ilçeye karşılık gelir. Boyutların her biri bir yatay eksene karşılık gelir ve her veri öğesi, boyutlar / eksenler boyunca bir dizi bağlantılı nokta olarak görüntülenir.

En sağdaki iki kırmızı çizgi, en yüksek cinayet oranlarına sahip ilçelerdir (St. Louis City ve St. Clair). PCP’nin sağındaki tek kırmızı çizgi St. Louis şehrini temsil ediyor. Sadece St. Louis Şehri en yüksek cinayet oranına sahip değil, aynı zamanda polis en çok parayı harcıyor ve en yüksek kaynak yoksunluğuna sahip. Bu grafik, bu üç değişkeni gerçekten perspektif haline getiriyor.

Sonuç olarak, GeoDa’daki veri keşif araçları beni tamamen şaşırttı.

Daha jeoistatistik tabanlı araçlarla nasıl çalıştığını görelim.

Coğrafi Uzayda Kalıp Bulma

Bu menüdeki temel fark, bu tür analizlerin coğrafi alanda nasıl yapıldığıdır . Histogramlar, dağılım grafikleri ve kabarcık grafikleri basitçe verileri analiz ederken, sonraki birkaç araç, ilçelerin ve özniteliklerin coğrafi olarak birbirleriyle nasıl ilişkili olduğunu anlar.

Ve her şey ağırlık yöneticisinde bitişikliği ayarlamakla başlar. Sınırı bir kraliçe veya kale bitişiğiyle doğrudan temas halinde olacak şekilde ayarladım. Bu, her ilçeye bağlanan komşuların sayısını etkiler.

İşte kraliçe bağlantısını ve komşu sayısını gösteren bir histogram :

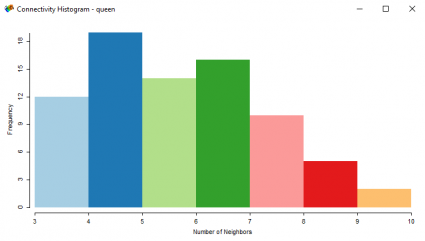
Kale bağlantısını ve komşuların sayısını gösteren bir histogram :

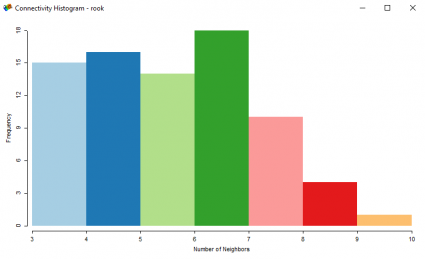
Çok benzer ama farklı. Geoda, kale ve kraliçenin komşularıyla nasıl bağlantı kurduğunu etkileşimli olarak görmeniz için bir harita sunuyor. Bu özelliği seviyorum.

Moran Dağılım Grafiği

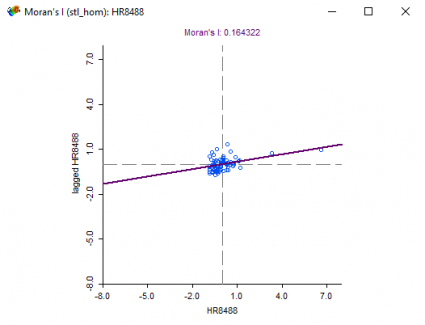
Ülkelerin birbirleriyle ilişkisini belirlediğimiz için, moran dağılım grafiği bunu hesaba katacak.

Pozitif uzamsal oto-korelasyon, Moran’s I + 1’e yakın olduğunda oluşur. Bu, değerlerin bir arada kümelendiği anlamına gelir. İken negatif mekansal otokorelasyon oluşur Moran Ben yakın olduğunda -1. Bir dama tahtası, Moran’s I’in -1 olduğu bir örnektir, çünkü benzer olmayan değerler yan yana.

Moran’s I için 0 değeri tipik olarak otokorelasyon olmadığını gösterir. Bu durumda, Moran’ın I değeri 0.16’dır, bu, cinayet oranlarının çok fazla bir arada kümelenmediği anlamına gelir.

Mekansal Otokorelasyon

Bir LISA Kümesi haritası seçtiğinizde, önemli bir Yerel Moran istatistiğini gösteren bir koroplet haritası oluşturacaktır. Parlak kırmızı, yüksek-yüksek değerlerini gösterir ve bu, yüksek benzer değerlerin kümelenmesini gösterir. Mavi ilçeler düşük-düşük değerler gösteriyor, düşük değerlerin bir arada kümelenmesini öneriyor.

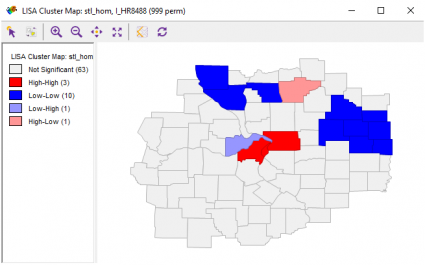
Kalan gri gölgeler önemli bir ilişki göstermez. Yüksek-alçak ve alçak-yüksek yerler uzamsal aykırı değerleri gösterirken.

Son olarak, GeoDa dört anlamlılık seviyesi üretir – p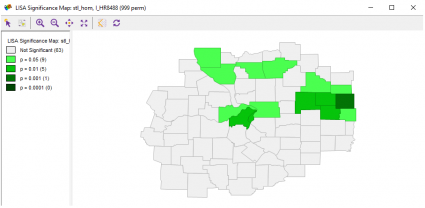

GeoDa, EB Rate ile tek değişkenli, diferansiyel ve yerel Moran I üretebilir.

Yerel G Kümesi Haritası

Son araç, verilerin nasıl kümelendiğini görmek için bir variatino’dur. St. Louis’in merkezinde, yüksek cinayet oranları ortada merkezileşmiştir. Kuzeydoğu kesiminde ise cinayet oranları çok daha düşük.

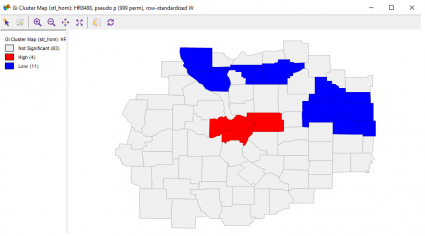
Bunun emlak endüstrisi ve St. Louis’e taşınmak isteyenler için ne kadar yararlı olduğunu bir düşünün. Bu durumda, G * Kümeleri haritası aynı sonuçları üretir.

Uzamsal Regresyon

Bir şehirde cinayet oranlarınız varsa, suç modellerinin arkasındaki faktörleri anlamak için mekansal regresyonu kullanabilirsiniz. Cinayet oranları neden St. Louis’in merkezinde yoğunlaşıyor? Polis harcaması mı? Kaynak yoksunluğu cinayetlerin yerini açıklayabilir mi?

Regresyon modellerinde yaygın olarak kullanılan bazı terminoloji burada.

• Bağımlı değişken (Y) : Neyi tahmin etmeye çalışıyorsunuz? (Cinayet oranlarının yeri)
• Bağımsız değişken (X) : Bağımlı değişkeni açıklayan açıklayıcı değişkenler. (Gelir, eğitim vb.)
• Beta katsayısı : Açıklayıcı ve bağımlı değişken arasındaki ilişkiyi yansıtan ağırlıklar.
• Kalan : Model tarafından açıklanmayan değer

Basit modelimizde cinayet oranları bağımlı değişkendir. Öte yandan, yüksek ve düşük cinayet oranlarını polis harcamaları ve kaynak yoksunluğu ile açıklamaya çalışıyoruz.

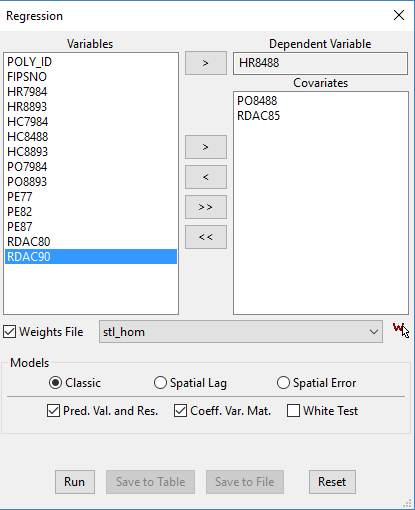
Regresyon Raporu

Çıktı tablomuz aşağıdaki gibidir:

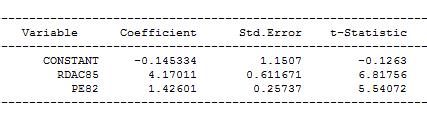
Regresyon modelimizdeki her katsayıyı değiştirdiğinizde, bu, daha yüksek kaynak yoksunluğuna ve daha yüksek polis harcamalarına sahip alanların matematiksel olarak cinayet oranları oluşturacağı anlamına gelir. Tahminin standart hatası, tahminlerin doğruluğunun bir ölçüsüdür. Bir regresyon çizgisinde, tahminin standart hatası ne kadar küçükse, tahminler o kadar doğru olur. T istatistiği ise katsayının standart hatasına bölünmesiyle elde edilir.

Akılda tutulması gereken bir başka istatistik, artıkların (gözlemlenen bağımlı değişken değerleri eksi tahmin edilen değerler) normal olarak dağılıp dağılmadığını gösteren Jarque-Bera istatistiğidir. Bu artıkları bir histograma koyduğunuzda, sıfır hipotezi bir çan eğrisine benzemesi gerektiğidir.

Buna ek olarak, çıktı tablosu, bir çoklu regresyon modelinde iki veya daha fazla yordayıcı değişken yüksek oranda ilişkili olduğunda çoklu doğrusallığı test etmenize de izin verir. Hesaplanan Moran I, regresyon artıklarının uzamsal olarak rastgele (uzamsal olarak otokorelasyonlu) olup olmadığını belirler.

GeoDa’daki diğer seçenekler, uzamsal gecikme modelleri ve uzamsal hata modeli için maksimum olasılık tahminidir.

 

GeoDa Son Düşünceler

Sen bir sürü gerekecek aha anları yürürken GeoDa içinde. Yalnızca CBS kullanıcısı olmayanlar için mekansal analiz ve istatistiklere nazik bir giriş işlevi görmez, aynı zamanda istatistikleri öğrenmeye çalışan kullanıcılar için yararlıdır.

Luc Anselin, GeoDa’yı ArcView 3.0 uzantısı olarak başlattı. Popülerliği nedeniyle, kendi açık kaynak veri keşif aracında yeniden çalışıldı.

Prototipiniz tam gelişmiş GIS paketiniz olmasa da GeoDa, ekonomi, sağlık, emlak ve daha fazlası gibi endüstriler için bir dizi heyecan verici analitik ve jeo-görselleştirme aracına sahiptir.

GeoDa ile jeoistatistiklerinizi test etmeyi denediniz mi? Aşağıdaki yorumlar bölümümüzde ne düşündüğünüzü bize bildirin.